Hur gjorde Arne Beurling för att forcera G‑skrivaren?

Arne Beurling lär ha varit förtegen om hur han verkligen bar sig åt i arbetet med att forcera G-skrivaren, och vid något tillfälle sagt att ”En trollkonstnär avslöjar inte sina trick”. Här publicerar vi ett resonemang av Carl-Gösta Borelius om hur Beurling kan ha burit sig åt. Carl-Gösta Borelius arbetade själv med forceringen av G-skrivarmaterial från 1941, och kom så småningom att sluta sin karriär som datachef på FRA. Denna redogörelse skrevs på 1980-talet och har sedan dess legat i FRA:s arkiv, och den publiceras nu för första gången.

Att det var Arne Beurling som knäckte den tyska G-skrivaren det är allom bekant, men hur han bar sig åt det har han aldrig avslöjat. David Kahn skriver att Beurling utgick från en enda dags trafik och dessutom möjligen hade kännedom om Siemens & Halskes patent. När Beurling vid sitt besök här på FRA i november 1976 blev tillfrågad om denna den första forceringen reagerade han egendomligt. Det verkade som om han ogillade att frågan ställdes. Han sade dock någonting om att han använde sig av treor och femmor i texten.

Nu är Beurling död och han kan därför inte rätta mig om jag spekulerar litet runt temat. Jag tror inte han behövde ha läst patentbeskrivningarna. (Kom ihåg i det som följer att 3=bokstavsskift, 4=sifferskift, 5=mellanslag).

Fjärrskriftslinjerna var långa och var utsatta för störningar. En störning gjorde att ett tecken förvanskades men det påverkade i allmänhet inte läsbarheten utom i de fall det ändrade tecknet blev 4, för då blev den efterföljande texten en följd av siffror och tecken i stället för bokstäver och alltså tämligen oläslig. Om störningen drabbade enbart mottagaren märkte avsändaren ingenting utan fortsatte sin sändning.

För att minska olägenheterna med detta hade operatörerna för vana - eller kanske var det till och med föreskrivet - att skriva 35 i stället för enbart 5 mellan orden, på så sätt återställdes verkan av en falsk 4 redan vid nästa ordmellanrum. Bokstavsskift, 3, blev ungefär lika högfrekvent som mellanslag, 5, och det kom att ha en stor betydelse för bearbetningen av G-skrivartrafiken.

Nutidens fjärrskrivare sätter automatiskt in behövliga skifttecken och skifttecken utöver dessa är svåra att åstadkomma men den skrivare som G-skrivaren var uppbyggd runt hade särskilda skifttangenter, och det var operatörens sak att skifta där det behövdes och han kunde också sända godtyckligt antal sifferskift (4) och bokstavsskift (3), allt efter behag.

Antalet parallella texter kunde vara mycket stort dessa tidiga dagar.

Sven T Johansson som var med då, har berättat om 20 - 40 parallella telegram. Det var alltså möjligt att avveckla texterna med hjälp av frekvensstatistik som om det vore fråga om en oordnad Vigenère. Stereotypa texter i början: QRV? (mycket vanlig), ERHALTEN SIE KLAR?, JA, KLAR osv, och studium av klartexterna mellan UMUM-en underlättade säkert detta.

En jämförelse mellan några högfrekventa klartexttecken ger:

Antag att man parallellavvecklat ett antal texter och att man i en kolumn finner tecknen 3, 5, Q, R och V.

Dessa tecken har utsatts för samma överlagring och samma transposition. (K=klartecken, ö=överlagring, C1=chiffertecken efter överlagringen, T=transposition. C2=slutligt chiffertecken)

Om vi nu jämför chiffermotsvarigheterna, C2, till de klartexttecken vi nyss jämförde finner vi:

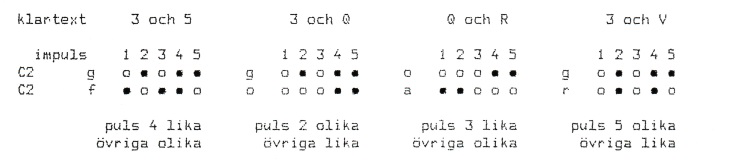
Vi ser att antalet lika respektive olika alltid är detsamma som i motsvarande klartextjämförelse; är i klartextfallet endast en impuls lika så är det så också i kryptofallet, men platsen för denna likhet kan mycket väl ha ändrats och pulsen kan också ha ändrat polaritet.

Detta märkte naturligtvis Beurling snart och det kunde han dra nytta av vid den fortsatta avvecklingen. I klartextfallet har 3 och 5 en impuls lika och fyra olika och måste så ha även i chiffrerat skick. För en gissad 3-a finns bara fem möjliga 5-or, och omvänt, en antagen 5-a ger endast fem 3-alternativ. Man kunde därför ganska lätt bestämma ordmellanrummen och det måste avsevärt ha underlättat avvecklingen och det var detta Beurling syftade på när han talade om treor och femmor. På motsvarande sätt ger en gissad 3-a endast fem möjligheter för respektive Q och V i QRV som var så vanligt i inledningen. Det är nog säkert att den rika förekomsten av 3 underlättade Beurlings arbete; det kom den i varje fall att göra under det fortsatta arbetet med G-skrivaren.

Och vidare låg slutsatsen, att en del av krypteringen består av en omkastning av fempunktstecknets impulsordning, nära till hands. Ett antal jämförelser som de här ovan ger också omkastningsordningen, transpositionen. I exemplet visar den första jämförelsen att impuls 3 gått till plats 4, den andra att 4 gått till 2, den tredje att 2 gått till 3 och den fjärde att 1 gått till 5 och då återstår ju för impuls 5 endast platsen 1.

Naturligtvis prövade Beurling i det här läget att återföra chiffertecknen till utseendet före transpositionen det vill säga till C1 och då gjorde han nästa iakttagelse. Förändringen från K till C1 består i att vissa av klartextbokstavens impulser har ändrat polaritet och för alla tecken i en kolumn är det alltid samma pulser som ändrats.

Nu får vi tänka oss att Beurling införde dessa iakttagelser på avvecklingspappret. På fem rader under de avvecklade texterna, satte han i varje kolumn en prick för de impulser som polvänts och en ring för de som ej ändrats. Eftersom den uppkomna fempunktskombinationen liknade en fjärrskriftsbokstav så kallade han den för överlagringsbokstav. Under detta skrevs permutations-ordningen och kallades för transposition.

Ett fragment av avvecklingsarket bör nu ha sett ut ungefär så här:

Avvecklingen fortsatte och när han avvecklat något 100-tal tecken och skrivit in överlagring och transposition gjorde Beurling en upptäckt som borde föranlett honom att ropa "Eureka" (såvitt bekant sprang han dock inte naken genom Stockholms gator). Mönstret av ringar och prickar i de fem raderna i överlagringen upprepades efter ett antal tecken och att han då antog att mönstren åstadkoms av stifthjul liknande hagelin-maskinens är ju förståeligt.

Så här långt hade pusselbitarna ramlat på plats nästan av sig själva. Nu återstod transpositionen och den fordrade kanske mera tankearbete.

Om vi betraktar transpositionskopplingen:

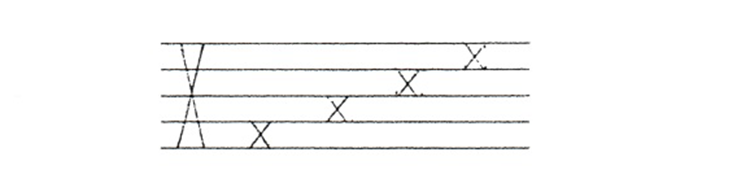
...så ser vi att det enda villkoret för att impuls 2 skall hamna på plats 3 är att den fjärde bryggan i ordningen ar öppen. Om bryggan är stängd kan inte puls 2 hamna på plats 3. Om nu bryggan styrs av ett hjul med jämn fördelning av aktiva och passiva stift s kommer puls 2 i hälften av fallen att hamna på plats 3 och i hälften av fallen på någon annan plats.

Och omvänt, om Beurling vid ett studium av hur impulserna hamnade på de olika platserna fann just detta att impuls 2 hamnade på plats 3 i 50 procent av fallen och på andra platser i de övriga fallen, så bör han ha dragit slutsatserna, dels att det fanns en förbindelse mellan platserna 2 och 3 dels att den förbindelsen kunde vara styrd av ett stifthjul och att fallet impuls 2 på plats 3 motsvarade den ena stifttypen och övriga fall den andra.

Beurling ritade nu in en ring under de transpositionsmönster där impuls 2 hamnat på plats 3 och en prick i alla övriga fall och fann att även den ring-prick-serien var periodisk.

Den fullständiga kopplingen och därmed utseendet av de återstående "stifthjulen" fick man fram genom hypotesprövning och så var der Geheimschreiber avslöjad.

Jag tror att det här antagna händelseförloppet är i huvudsak riktigt, Beurling kan inte ha undgått att göra de iakttagelser som jag har visat på och han måste då också ha dragit de i många fall självklara slutsatserna av vad han sett. Analysen är en nästan oundviklig följd av att systemet tillät parallellavveckling.

Med det här vill jag på intet sätt förringa Beurlings insats, det är lätt att vara överlägsen när man har facit i sin hand. Men kanske kan Beurlings ovilja att avslöja hur han bar sig åt ha berott på att han visste att det han gjort mycket väl hade kunnat göras av någon annan. Han lär ju också ha svarat någon som undrat hur han gått till väga: "En trollkonstnär avslöjar inte sina trick".

Beurling var en stor man och gjorde bestående insatser på många områden inom kryptologien. Och han var den som knäckte den tyska G-skrivaren. Den äran ska ingen ta ifrån honom.